1-1 Physics: An Introduction
- Physics is concerned with describing the interactions of energy, matter, space, and time, and the mechanisms underlying these concepts.
- Physics can be used to describe how different objects function. For instance, GPS systems use motion, distance, and speed to determine the approximate travel time between locations.
- This field of study also serves vital functions in many other scientific fields.
- Chemistry - interactions between atoms and molecules (such as collisions)
- Geology - analyzing earthquakes, heat transfer in the earth
- Biology - describing properties of cells, heat and work of living beings
- Models are used to represent things that may be difficult to display directly.
- Theories are explanations of patterns that can be supported using scientific evidence that is verifiable.
- Laws describe a general pattern seen in nature, using notation such as mathematical equations.
- The scientific method is a process used to gather information regarding a question that needs to be answered.
- Observation
- Question formation
- Research
- Hypothesis formation
- Hypothesis testing
- Result analysis
- Conclusion
- Physics is a field that has evolved from many different fields, through the observations and analysis made by a wide variety of researchers across history.
 |
 |
 |
| Aristotle: philosopher, 384-322 BC | Galileo Galilei: astronomist and mathematician, 1564-1642 | Niels Bohr: physicist, 1885-1962 |
1-2 Physical Quantities and Units
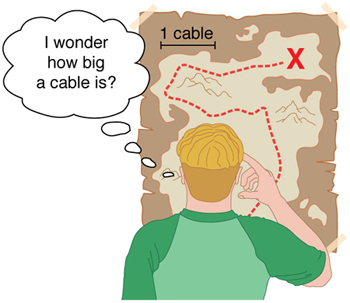
- Physical quantities of objects require units, or standardized values that depend on the concept being measured.
- SI units (metric system):
- Time: second (s)
- Length/Position: meter (m)
- Mass: kilogram (kg)
- Velocity: meters per second (m/s)
- Acceleration: meters-per-second per second or meters per second 2 (m/s 2)
- Force: Newton (N = kg m / s 2)
- Energy: Joule (J = kg m 2 / s 2)
- When converting from one unit to another, you must multiply the quantity by a conversion factor (such as 1 km / 1000 m) in such a way that the original units are cancelled out and the new units are left.
- Example 1:
- Example 2:

1-3 Accuracy, Precision, and Significant Figures
- Accuracy: how close a measurement is to the correct value.
- Precision: how close together repeated measurements are (regardless of correct value).
- Measurements may not always be both precise and accurate; repeated measurements may be close together while being far from correct, or they could be near the correct value without being near to each other.
- Measurement tools each have different levels of precision, and their measurements can only be done to a certain number of digits (significant figures).
- Significant figures must be kept track of when finding measurements and making calculations. The last digit is the first digit with some uncertainty.
- Zeroes: significant, except when they are placekeepers.
- Multiplication and division: Result must have same number of significant figures as the quantity with the least significant figures.
- Addition and subtraction: Result must not have more decimal places than the quantity with the least significant figures.
1-4 Approximation
- Quantities can often be estimated using formulas where the input has limited accuracy. These approximations can be used as estimations that are relatively close to what the actual value is. They can also be used to analyze results and see if they are in line with the approximations.
- Example: to approximate the height of a 39-story building, we can use approximations. One person is about 2 meters tall, and one story is about the height of two people.
- 39 stories x (2 people/1 story) x (2 meters/ 1 person) = 156 m, meaning the building is about 156 meters tall.
