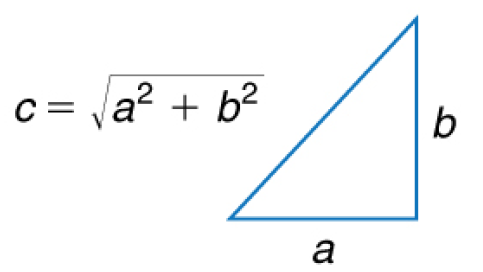Chapter 3: Two-Dimensional Kinematics
Introduction
- Most motions in nature follow a curved path rather than a straight line.
- One-dimensional kinematics (such as those from Ch. 2) can easily be extended to two- and three-dimensional kinematics.
3-1 Kinematics in Two Dimensions
- Vector: a quantity with both magnitude (length) and direction (angle).
- Vectors can be used to describe the path of objects in two dimensions
- Example: one vector may show the horizontal component of motion, while another shows the vertical component.
- Two perpendicular vectors form a right angle. If we wish to find the straight-line path between the start and end points of these vectors, we can use the Pythagorean theorem.
- a2 + b2 = c2
- a and b are the magnitudes of the perpendicular vectors, while c is the magnitude of the hypotenuse.
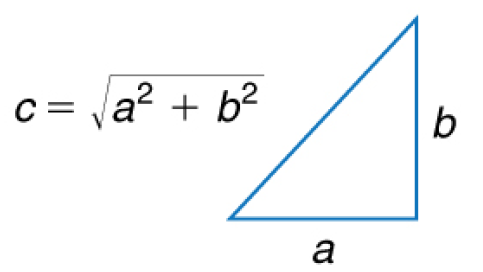
- The horizontal and vertical components of motion are independent of each other, and neither affects the other
3-2 Vector Addition and Subtraction: Graphical Methods
- Given a vector V, its magnitude is represented by the variable in italics V and its direction is represented by θ.
- Adding vectors graphically: place all vectors head to tail, and draw the resultant vector.
- Subtracting vector graphically: subtracting a vector is like adding its negation. Negate the vectors that will be subtracted, then add all the vectors together by placing them head to tail and drawing the resultant vector.
- Vectors are often separated into their perpendicular component vectors to be analyzed.
3-3 Vector Addition and Subtraction: Analytical Methods
- Trigonometry is used to determine the magnitudes and directions of vectors

- Say there exists a vector, vector A, with direction θ. It is composed of two perpendicular vectors added together: its x-component (Ax) and its y-component (Ay).
- Magnitude of Ax: Ax = A cos θ
- Magnitude of Ay: Ay = A sin θ
- Magnitude of A: A2 = Ax2 + Ay2
- Direction θ: θ = tan-1(Ax / Ay)

3-4 Projectile Motion
- Objects thrown into the air are called projectiles, and their path is called the trajectory. Assume air resistance is negligible for now.

- Recall that motions along perpendicular axes are independent of each other.
- This allows us to analyze motion by splitting it into two motions: one vertical, one horizontal.

- Assume that gravity only affects motion in the vertical direction.
- ay = -g = -9.80 m/s2
- ax = 0
- Total displacement of a projectile can be found by using a vector s that's composed of perpendicular x- and y-components. Velocity is v.
- Horizontal motion
- x = x0 + vxt
- vx = v0x = constant velocity
- Vertical motion
- y = y0 + 1/2(v0y + vy)t
- vy = v0y - gt
- y = y0 + v0y - 1/2(gt)
- vy2 = v0y2 - 2g(y - y0)
- Total displacement and velocity (of the original vector s)
- s2 = x2 + y2
- θ = tan-1(vy / vx)
- v2 = vx2 + vy2
- θv = tan-1(vy / vx)
- Maximum height of a projectile
Compare the purple square with its x-component (blue) and y-component(red)
3-5 Addition of Velocities
- Velocity is a vector, so the same rules of vector addition explained above apply to them.
- The velocity of an object can be split into its component velocity vectors along the x- and y-axes.
- Given a velocity vector v with direction θ that is made up of component velocity vectors vx and vy:
- vx = v cos θ
- vy = v sin θ
- v2 = vx2 + vy2
- θ = tan-1(vy / vx)